Interpolation in pure python
Posted on 23 February 2013
A long while ago, I wrote a script for
matplotlib that later (after lots of work by
Tony Yu and others) became the matplotlib
streamplot
function. This function generates plots that are constructed out of
streamlines of a flow, in such a way as to fill the domain uniformly
with such streamlines. I wrote the script to plot winds in the
tropical upper troposphere/lower stratosphere where there is a lot of
divergence and convergence (principally caused by convection over the
western Pacific and subsidence over the eastern Pacific.)
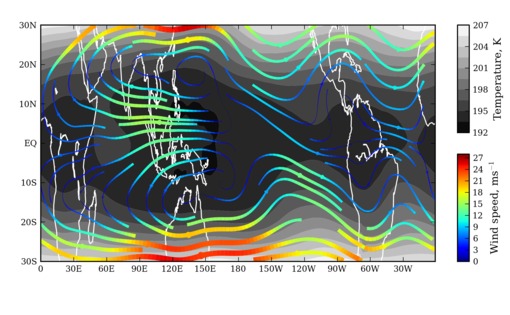
The streamplot algorithm uses an adaptive 1st/2nd order
Runge-Kutta
scheme and linear interpolation of the velocity field to integrate the
streamlines. This was implemented in pure python, which I originally
chose to do because the portion of the algorithm responsible for
ensuring an even domain-filling distribution of streamlines imposes a
very strange termination condition on the integral that does not fit
well with the integrators in scipy. In addition, matplotlib does not
depend on scipy.
I initially expected a pure python algorithm to be incredibly slow, so
I used a very simple interpolation scheme. Any interpolation scheme
interpolating some data D[i] defined at points x[i] on to the
target point x0 is composed of two steps; first, the algorithm must
identify the nearest grid points to the target point. Second, the
interpolator must apply the appropriate interpolator to those
neighbouring points.
The second step is usually trivial to implement, but the first step is
non-trivial in general. The first step becomes a lot simpler when we
restrict ourselves to a regular grid with spacing dx as we can then
find the index i of the point just above x0 by rescaling and
casting to an integer
i = int(1 + (x0 - x[0]) / dx)I thought this was probably the fastest way of implementing an
interpolator and so used this technique to implement the interpolator
in streamplot. However, it added some complexity to the algorithm
and, most importantly, imposed a restriction that only regular grids
(i.e. grids with evenly spaced axes) could be used. For my original
purpose, this was not a problem but it is clearly a rather serious
limitation in general.
Recently I have been hitting this limitation and decided over the last
couple of evenings to try to free streamplot of this limitation. To
generalise the first interpolation step to work with any x[i], a
search is needed to find the smallest i such that x[i] > x0. Any
pure python search algorithm would be too slow. Using argmax to do a
linear search is an option:
i = numpy.argmax(x[i] > x0)However, this does not scale well with the length of each dimension and is too slow in this context.
Looking through the standard library, I came across the bisect
module which implements the
interval bisection method
for searching ordered lists and arrays – exactly what I needed
to do. Implementing this search is really simple; it’s just
i = bisect.bisect(x, x0)This method is really fast – way faster than I expected. After re-implementing the streamplot integrator and interpolator to use this type of interpolation, typical plotting times were barely increased.
Here is an example of the new script in action with a very non-uniform vertical grid spacing:
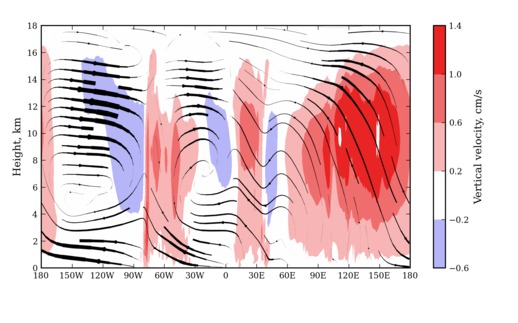
(This plot shows the boreal winter average zonal and vertical winds in the inner tropics.)
The new script is available here. Feel free to try it out if you need to do streamplots with uneven grids. Please note that this is a work-in-progress and so use with caution :-)